In the lighting world, there has recently been a lot of commotion about the low power factor of certain lamps, especially LED lamps. You often hear that the power factor is the same as the cosine phi(cosφ). Sometimes you hear that a low power factor can be compensated by a capacitor or capacitor battery. Others say that a low power factor is adverse and inherent feature of an LED. What is the link between harmonics and the power factor? This article tries to explain the concepts cosφ, power factor and harmonics in a slightly more scientific way. After reading, it must be clear that these terms are not the same.
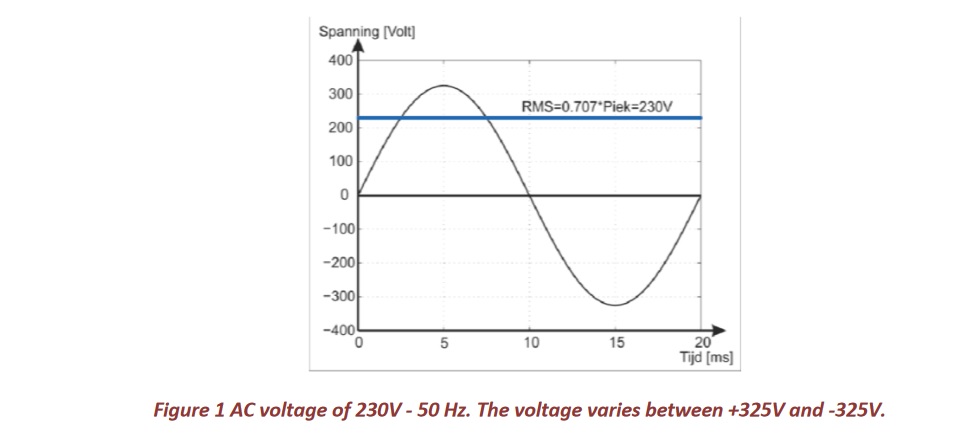
All consumers connected to the electrical network will receive an alternating voltage of 50 Hz. The waveform of an alternating voltage is shown in Figure 1. The voltage varies between a minimum and a maximum value according to a sine, as shown in black. In a 50 Hz network, this sinusoidal wave is fully run 50 times per second (i.e., one period is 20 milliseconds). The signal drawn is an alternating voltage of 230V. Why does the signal not fluctuate between -230V and + 230V, but between -325V and + 325V?
This is because we always use effective values in electrical engineering (also called RMS values). By an effective value of a periodic alternating current or voltage, we mean the value of a constant current or voltage which, in a resistor, on average, develops the same electrical power as the original signal. At a sinusoidal signal, the RMS value equals 0.707 times the maximum value. In our example, a DC voltage of 230V will generate equal power in a resistor as a sinusoidal AC voltage which varies between -325V and + 325V.
If a consumer is connected to an electricity grid, then there will be power flowing. Previously, there were mainly linear consumers. These are consumers whose recorded current is also sinusoidal. In Figure 2, the current used by a resistor (e.g., a bulb or electric heater) and an induction motor is shown. The current is also sinusoidal, but in the righthand figure the current is shifted.
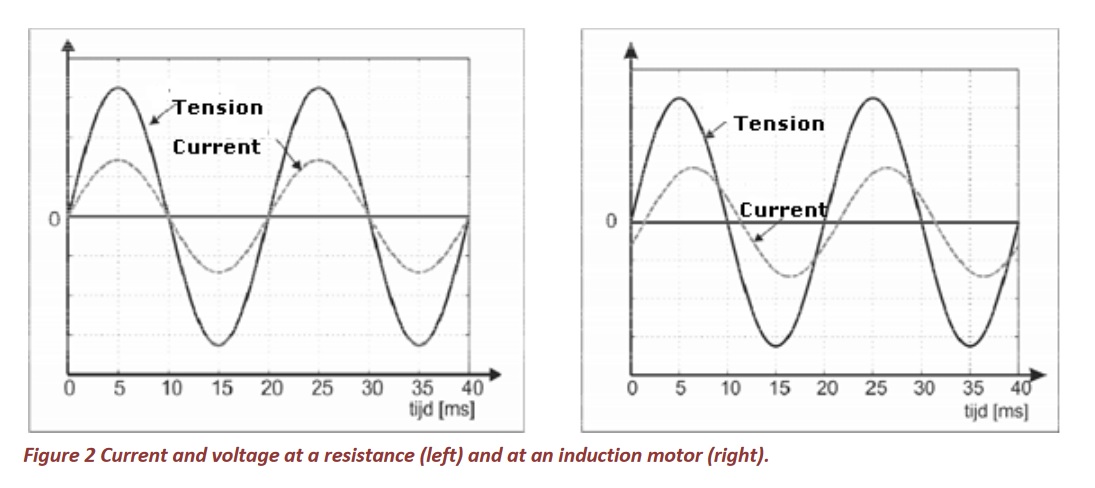
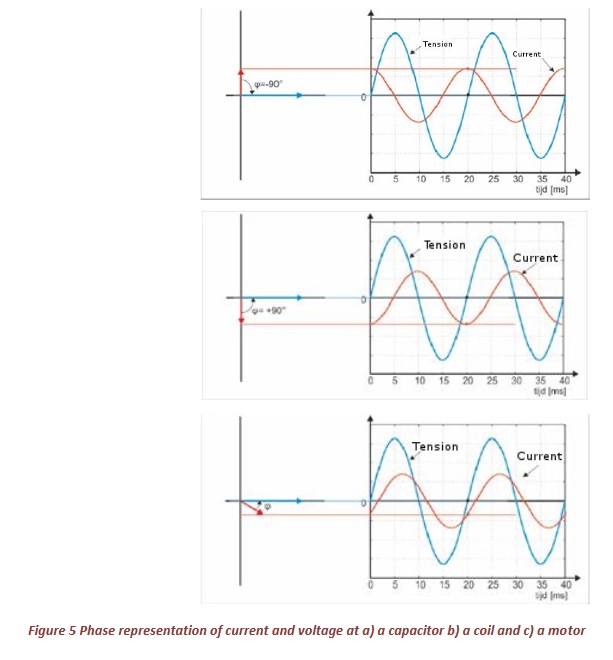
Calculation and thinking with sinusoidal time waveforms is complicated and cumbersome. Therefore, currents and stress are often represented by arrows (phases, vector rotation). When current and voltage cross each other at 0 and at the same time reach a maximum and minimum, we say that current and voltage are in phase (as in Figure 2, left). This is the case with resistance loads such as heating elements and glow and halogen lamps. The arrows of the current and voltage then coincide (i.e., have the same direction), see Figure 3. How do we get a phasor (or arrow)? A phasor is a rotating vector (or arrow) with length equal to the amplitude. The speed at which it rotates is proportional to the velocity (or frequency) of the wave. Between times t0 and t4 of Figure 3, one period passes through (and the wave starts again); In the phasor figure, the arrows are at the times t0 and t4 together and they run exactly 360° on t4. At time t1, the period for a quarter has elapsed. The arrows of voltage and current are thus drawn at an angle of 360° / 4 = 90°. Analogous to time t2 where the arrows are drawn at 180° and for time t3 where the arrows are drawn at 270°. At time t4 the wave is complete and the arrows are drawn at 360 °, ie they coincide with the arrows at time t0. Indeed, the wave starts again.
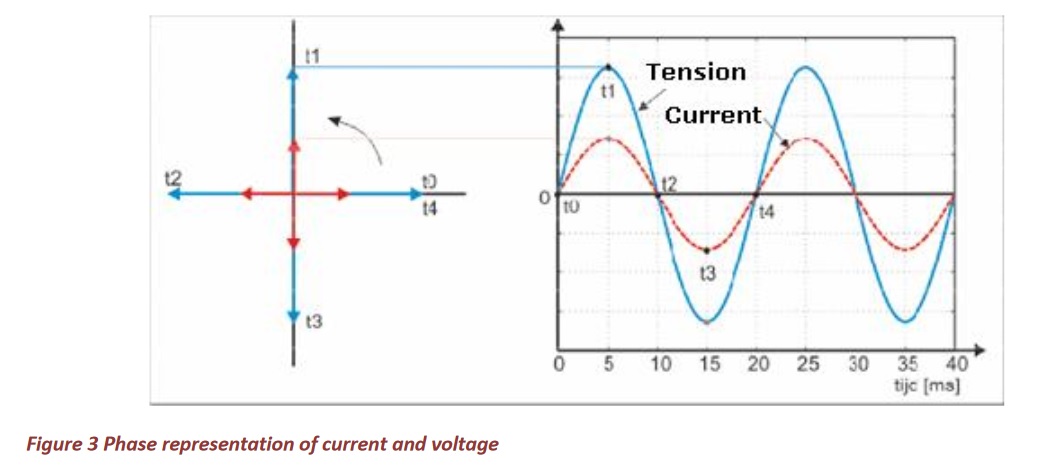
When we know the arrows in a single moment, we know where they are located at any other moment. Hence, the arrows are usually drawn at t0. The phasor representation of the current and voltage at a resistive load (current and voltage in phase) is shown in Figure 4.
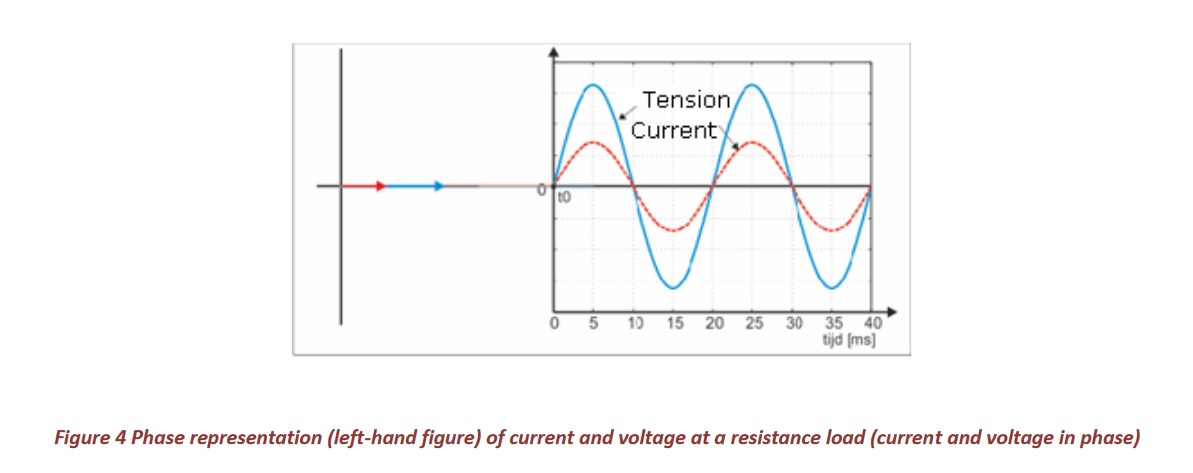
For most consumers, the current will not be in phase with the voltage. This is among other things connected with motors and fluorescent lamps connected to a conventional ballast with the input capacitor not connected. In Figure 5, the currents and voltages are represented by a capacitor, coil and an inductive consumer such as a motor. The angle between the voltage and the current we call the phase angle phi (represented as φ) (positive angle when voltage leads to current as in a coil). The angle φ at a resistor (Figure 4) is of course 0 °.
A consumer connected to the net switches electrical energy to another form of energy. Thus, a lamp converts electrical energy into light and a motor converts an electric power to mechanical energy to drive a pump, for example. The electrical energy we consume we pay on the electricity bill. The electrical energy consumed by a consumer during a time interval Δt is equal to
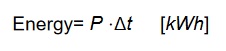
In this case P represents the active capacity or power. The active power is expressed in watts [W]. The energy is usually expressed in kWh. The price per kWh of energy (asset capacity is the time interval) is approximately 0.22 € for private customers. For example, a 60 W light bulb will have consumed 60 kWh for its lifetime of 1000 hours, which amounts to 13.2 €. The active power P depends on the voltage and current but also of the phase difference φ between these two magnitudes. The active power P can be written as:
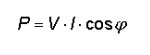
The active power is thus also dependent on cosφ (cosine phi)! for the calculation of a cosine. Consider a consumer connected to a 230 volt mains voltage. Suppose the power consumed is 230 watt. If the current is in phase with the voltage (φ = 0) then the current is equal to 1 ampere. If the current and voltage are not in phase and the phase difference, for example, is 60°, Then the same power of 230 W requires a power of 2 amps (being 230/(230 * cos 60°))! The customer pays in both cases the same amount (because he only pays for the active power P) but the current is twice the size! Another power that is often used is the apparent power S. This power is defined as the product of the effective value of voltage and current. Unit VA or VoltAmpere: S=V.I. Apparent power is important because it determines the size of transformers and fuses. Electrical appliances must be able to handle the voltage (V) and, on the other hand, resist the current (I). The apparent power combines these two factors.
Electricity is generated in power plants and consumed by electricity customers. The energy transport is via electricity cables. These cables always have one - although small - resistance. When current passes through a resistor, there is always a conversion of electrical energy in heat. Energy transport is therefore always associated with energy loss. These energy losses in cables are proportional to the resistance of the cables R and to the square of the current flowing through: Cable losses=R I². The power associated with this energy loss must be provided by the producers and distributed by the network administrators (electrical network administrators including Eandis, Infrax for individuals) while customers do not pay this directly (via the net rates).
When consumers take on a power P, the power plants must supply a power equal to this power P plus the cable losses. Therefore, a transmission performance can be defined as follows:
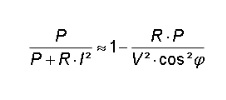
The transmission performance is greater as: • the resistance of the cables is smaller -In practice, mainly conductors with high conductivity such as copper or aluminum are used
• the voltage is higher – therefore, transportation over long distances is done with high or medium voltage (high voltage in Flanders is typically, 380kV, 150kV, 70kV or 36kV)
• the cosφ is higher
At a given active power, the current through the conductors and the cable losses will decrease as the cosφ is greater. This also means that with a given cable diameter and mains voltage, more power can be transported as the cosφ of the consumers is higher. Therefore, (distribution) network administrators will charge higher rates to non-private consumers who consume energy at low cos φ. These consumers force the companies to provide active assets that are associated with currents in transmission lines that are larger than strictly necessary and therefore with higher cable losses. Indeed, these consumers provide for a greater load of transformers, cables and power stations and therefore for more costs. Non-private customers will always have to ensure that the total recorded flow of their business is at all times in phase with the mains voltage. In practice, cosφ must be greater than 0.95 (which is the same as an angle φ not greater than 18 °). To achieve this, one will usually places a capacitor battery. Consider Figure 6 for this. Without a capacitor battery, the company charges a current that is not in phase with the mains voltage. This flow typically precedes the tension, usually due to the large number of engines in companies. The recorded active power P is, as seen, written as V.I.cosφ.A capacitor battery will take a current that precedes on the tension–see Figure 5, case a The total current flowing to the grid consists of the operating current I on the one hand and the current through the capacitor bank Icond on the other hand. The current Inet is the sum of these two contributions and is shown in Figure 6. When the capacitor battery is properly regulated, the total current flowing to the grid will be (substantially) in phase with the mains voltage, leaving the cosφ close to 1.
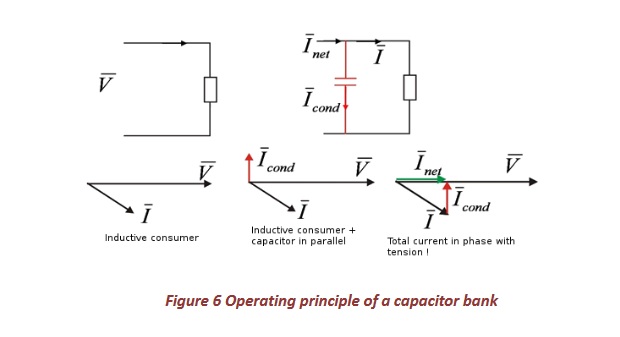
It is important to note that Inet < I causing the current flowing into the grid to be smaller with a capacitor bank than without. Therefore, the net losses will indeed be smaller. However, the company’s active power remain unchanged:
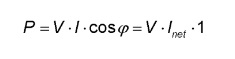
From this all we can realize that the efficiency of the energy transfer is also determined by the cosφ. In general, we can say that the return on energy transfer η is as follows:
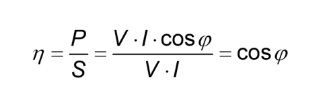
Figure 7 shows a picture of a capacitor battery.

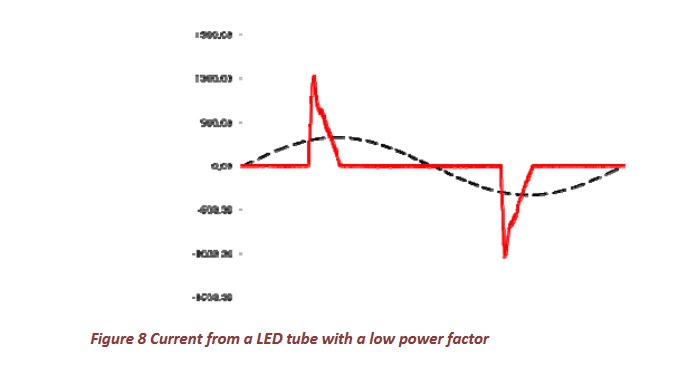
Due to the rise of power electronics, there are many consumers who do not absorb sinusoidal power from the grid. A typical example of a nonlinear current is shown in Figure 8. This is the flow of an LED tube but there are many consumers with such a waveform
Any random periodic signal, however distorted, can be written as a sum of sinusoids (by fourier transformation). Now take the signal represented in Figure 9 (red curve - left). This signal can be written as a sum of a 50Hz sinus with amplitude 1 (black curve) along with a 250Hz sinus with an amplitude of 0.1 (blue curve).
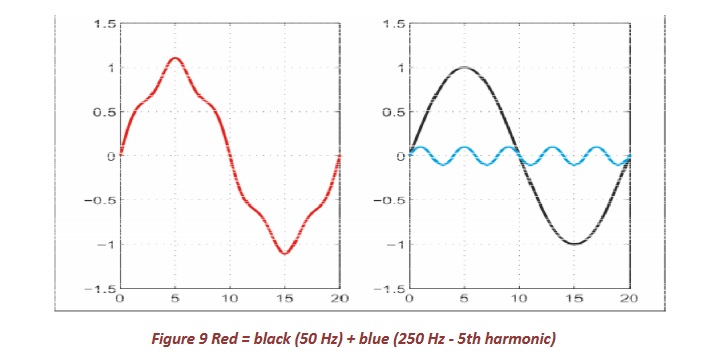
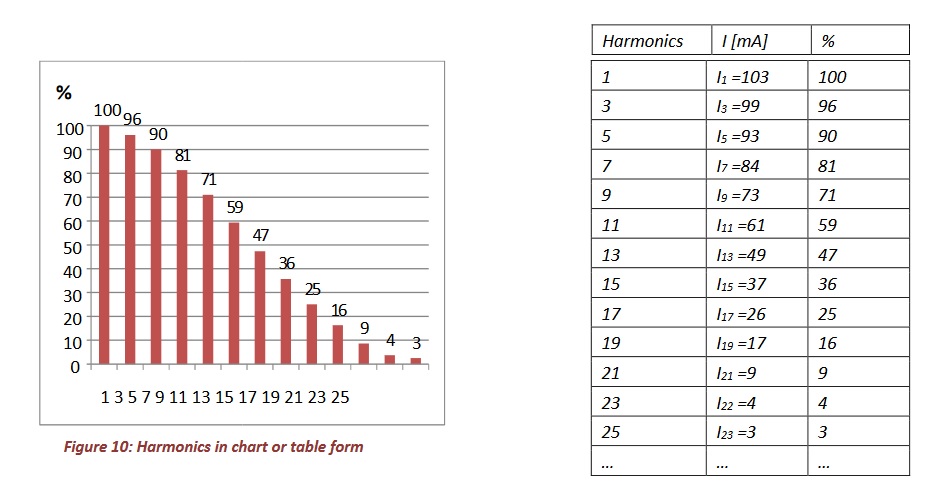
The sinuses are always a multiple of 50Hz. We call this harmonics. Such is a sinus of 150Hz a 3rd harmonic (3 * 50Hz is 150Hz) and a 250Hz sinusoidal 5th harmonic (5 * 50Hz = 250Hz). The deformed signal of Figure 9 contains, besides the 50Hz component, also a fifth harmonic. Usually, the harmonics are set as in Figure 10, the size of each harmonic being shown in graph or in tabular form. Figure 10 shows the harmonics of the current through the LED tube in Figure 8 (the phase angle of the harmonics is usually omitted; for I1 the measured phase angle is 8 ° in this example).
The active power P of a consumer who takes a non-sinusoidal current from the network can be written as follows (we assume no DC is present):
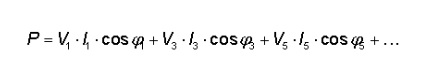
Thus, the active power P is obtained by taking the sum of the power generated by the mutual operation of the sinusoids of the same frequency. With two different frequency sinuses, no power is supplied. In practice, it now appears that the network voltage can be regarded as pure sinusoidal by a good approximation (due to the negligible net impedance). As a result, the mains voltage usually contains negligible small harmonic components so that we can approximate that all harmonics in the voltage are almost equal to zero. For example, take the LED Tubes of Figure 8. Suppose we connect this LED Tubes to a pure sinusoidal power of 230V. Since the mains voltage is pure sinusoidal (and thus does not contain harmonic components) the power is equal to:
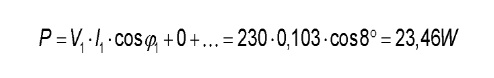
The harmonic components in the current thus do not contribute to the active power and to the energy consumption consumed! However, harmonic currents must be delivered. As we have also mentioned with the term cosφ, the current here is also higher than strictly necessary to transfer the same active power P. This higher current causes additional losses in pipes (cable losses = R.I²). The effective value or RMS value I of the current is determined in non-sinusoidal current as follows:
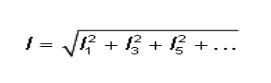
The current of the LED tube in our example is (see Figure 10 for the values):
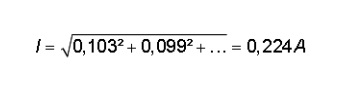
If the current is sinusoidal and in phase with voltage then a current of 0.102 A (= 23.46 / 230) is sufficient! A measure of current distortion is Total or Harmonic Distortion (THDI), defined as:
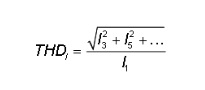
In other words, for a pure sinusoidal signal, there are no harmonic components and therefore the THDI is equal to 0. The more harmonics, the higher the THDI and the greater the deviation as compared to the pure sinusoidal signal. The LED tube THDI in the example is 130%.
In pure sinusoidal signals, we have seen that the efficiency of the energy transfer is equal to the cosφ. However, in non-sinusoidal signals this is no longer valid. However, we can still write the return on energy transfer as:

As already mentioned, the voltage in practice can be regarded as pure sinusoidal by good approximation (eg due to the small net impedance). We can therefore approximate that all harmonics in the voltage are substantially equal to zero. However, the currents can be highly deformed. With this in mind, we can write the power factor λ as:
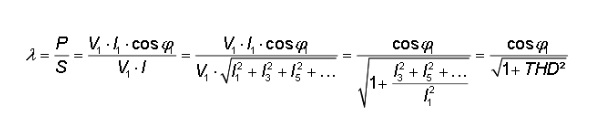
In other words, the power factor depends on both the cosφ1 and the deformation (THD) of the current! Note that if the current is pure sinusoidal, the power factor is equal to the cosφ1 (because the THD of the current is then 0). The term cosφ1 is called the displacement power factor or abbreviated dPF. The power factor, a measure of the efficiency of the energy transfer, can be low because of:
• a low cosφ1 (dPF)
• high current deformation (high THDI)
• a combination of both!
Thus, the power factor PF can be equal to 0.71 because:
• A pure sinusoidal current 45 ° out of phase with the voltage (cos45 ° = 0.71, THD = 0) or I
• a current that is strongly deformed THDI = 100% but whose ground wave (this is the 50Hz component or first harmonic I1) is in phase with the mains voltage (cosφ1=1) or
• A deformed current with THDI = 70% whose groundwave is 30 ° out of phase with the tension
As we mentioned earlier, too low a cosφ can be compensated by placing a capacitor battery (see Figs. 6-7). On the other hand, the THDI, and by extension the power factor, can not be compensated just by placing a capacitor or capacitor battery! It is often said that a too low power factor is compensated or can be made by a capacitor. This is not the case when the current is strongly deformed. Due to the capacitor, the power factor may even worsen! This is the case when your cosφ1 value is (almost) 1. If the THDI of the current is 100% then at cosφ1 =1, the power factor PF equals 0,707, being
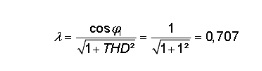
With a capacitor the cosφ1 (dPF) will be smaller than 1, which will decrease the power factor even more! Reduce current distortion (and reduce THDI) can only be achieved by adjusting the steering electronics. In practice, the customer can not do anything about this and this is a task of the manufacturer of the power consuming devices. Why do we then see so many energy-saving lamps and LEDs that absorb a strong distorted current with very high THDI values and a low power factor? This has little or nothing to do with the LED or energy saving lamp. For lamps below 25 W, no limits are required in the European Standard NBN-EN61000-3-2 "Electromagnetic Compatibility (EMC) - Part 3-2: Limit Values - Limit Values for Emission of Harmonic Current (Input Current of the Appliances 16 A per phase)" and this because the power and thus the injected currents are relatively small. Most manufacturers therefore take little or no measures to reduce the low power factor. Why would they? It only makes their products a bit more expensive. However, many little ones can make one big one: 1 LED lamp hardly affects the electrical network, many thousands of lights can indeed affect! In the event of imminent problems, the limits for harmonics may become stricter in the future.
For the distribution network administrator A low power factor PF is primarily a problem for (distribution) network administrators. Consumers with a low power factor are forcing the companies to provide active power that is associated with currents in the cables that are larger than strictly necessary, thus resulting in greater cable losses and a greater load of transformers, cables and power stations. To illustrate this, we give the following example. Consider a copper cable with a section of 4 mm² and a length of 25 m5. The cable losses are calculated on lamps with a) A power of 2000 W, the current being sinusoidal and in phase with the voltage. b) A power of 2000 W, the current being sinusoidal but not in phase with the voltage The angle φ is 60°. This consumer, for example, has a poor cos φ equal to 0.5. c) A power of 2000 W, the current being strongly deformed (as in Figure 8) with a THDI of 130% and a cosφ1 =1. The voltage is 230 V. Each cable has a resistance of 0.219 Ω. The current and cable losses for the three cases are shown in Table 1.
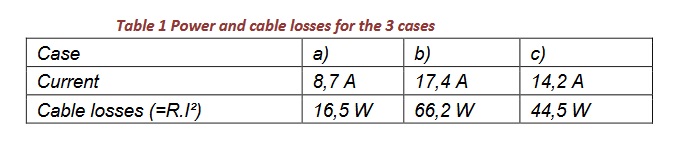
In case b), cable losses can easily be reduced by placing a capacitor. With full compensation (φ = 0 or cosφ = 1) the cable losses will decrease to a), being 16.5 W. Do you understand why a bad cosφ is being fined? For case c), no easy compensation is possible! If the lamps were burning in case of c) 4000 hours a year, this means that 178 kWh of energy is lost in the cable every year, which would only be 66 kWh if the power factor was equal to 1. In the calculation, we have neglected that the cable resistance and thus the losses rise as the temperature rises. Also, we do not take into account the frequency dependence of the resistance. This means that the above figures are underestimated. An additional aspect of the larger currents is a greater voltage drop in the distribution network, resulting in greater voltage variations. For the customer For private customers, a low power factor is not a problem because they only pay the active power. The harmonics do not contribute to the active power and the counter does not ‘see’ the harmonics. For non-private customers, a low power factor of lamps is usually not a problem either. Unless so many lamps are installed with a low power factor (due to a high THDI) that the pipes or transformers overheat and overload. Another aspect is that streams with certain harmonic orders (including 3rd) in the three phase conductors are in phase and are thus added to the zero conductor of the LS network. This may lead to overload of the zero conductor, which sometimes has a smaller section than the phase conductors (with older cables). On the other hand, a low power factor may also give rise to greater voltage variations (in the case of poor cos phi) or greater harmonic pollution of the voltage (at large THDI). All aspects of the voltage must certainly remain within the limits of the EN50160 standard.
This article was written in the context of the project 'Green Light Vlaanderen': Energy-saving with better light '- IWT 070488, carried out by the KAHO Sint-Lieven and WTCB Lighting Technology Laboratory.
- Accessoires
- Bay lighting
- Bulbs
- Decorative
- Downlighters
- Fixtures
- Bollard IP66
- Continuous Linear Pendant Led Light
- Eco Linear Led Light
- Farming industry fixture IP67
- GU10 AR111 E27/PAR 30 trackfixtures
- Inground induction luminaire 9w 12w
- LED chipboard fixture IP65
- LED Plug&Play fixture IP66
- Landscape LED light IP65
- NUD E27 lamp holder
- Polyester Fix Batten
- Ball resistant sports fixture
- Floodlight
-
Led strips
-
IP20 Led Strips
- Low Power, IP20, 2835 60LED/m, 4.8W/m, 8mm PCB
- Low Power, IP20, 2835 120LED/m, 9.6W/m, 8mm PCB
- IP20, 2835 60LED/m, 14.4W/m, 10mm PCB
- IP20, 2835 120LED/m, 19.2W/m, 10mm PCB
- RGB, IP20, 5050 60LED/m, 14.4W/m, 10mm PCB
- IP20, 2110 120LED/m, 7.2W/m, 4mm PCB
- IP20, 2110 180LED/m, 12W/m, 10mm PCB
- IP20, 2110 240LED/m, 15W/m, 10mm PCB
- IP20, 2110 300LED/m, 18W/m, 10mm PCB
- Nature led strip with violet chip, IP20, 2835 70LED/m, 9.6W/m, 8mm PCB
- Nature led strip with violet chip, IP20, 2835 140LED/m, 19.2W/m, 10mm PCB
- Tunable ledstrip 98CRI 2000K~3000K, IP20, 168LEDs/m, 16.8W/m, 10mm PCB
- Ultra long led strip 10~100m IP65
- IP67 Neon Led Strips
-
IP20 Led Strips
- Machine and desk lights
- Panel
- Spot
- Streetlight
- Tubes
- Tracklight

















